Tag: Eight Queens

This is the fourth and final part of the series showing how to solve the “Eight Queens” chess puzzle, using a database design and SQL. The main idea is to design using natural language and concepts of domains, predicates, constraints, sets, set operations, and relations.

Links to all previous and this post’s code.

Part	Main Topic	Code (pgSQL)
1	Domains, Types	part 1
2	Predicates, Constraints, Relations	part 2
3	Propositions and Facts	part 3
4	The Algorithm and the Solution	part 4

Algorithm

Say we place a queen, Q1, on square c5, Continue reading “Eight Queens in SQL [4]”

The third article in the series.

Links to all previous and this post’s code.

Part	Main Topic	Code (pgSQL)
1	Domains, Types	part 1
2	Predicates, Constraints, Relations	part 2
3	Propositions and Facts	part 3

Relation Values

To populate tables simply run the code; it is self explanatory. You may want to keep an eye on the model while reading the code.

Propositions and Facts

A proposition is a declarative sentence, Continue reading “Eight Queens in SQL [3]”

This is the second article in the series; the previous one introduced the problem and specified domains.

Links to all previous and this post’s code.

Part	Main Topic	Code (pgSQL)
1	Domains, Types	part 1
2	Predicates, Constraints, Relations	part 2

The Essence

The idea is to describe the problem using natural language and concepts of domains, predicates, constraints, relations and keys; here are a few simple rules to keep in mind.

From predicates and constraints to relations and keys

• A predicate variable — from a specific domain — maps to an attribute of the relation.
• Internal (to predicate) uniqueness constraints map to keys of the relation.
• External (to predicate) inclusion constraints map to foreign keys between two relations.
• A predicate and the matching relation represent — evaluate to — a set of facts about the universe of discourse (the problem).
• A predicate and the matching relation should not be separated, otherwise information will be lost, for all practical purposes.

Continue reading “Eight Queens in SQL [2]”

The puzzle is to place eight queens on a chessboard so that no two queens attack each other. The problem is old and has been well studied, the Rosetta Code has solutions for more than 80 programming languages, SQL included.

However, the Rosetta’s SQL solution is implementing a recursive algorithm in SQL, as opposed to a relational approach. In this article I will use a relational design approach to the problem, and then translate that to SQL. The main idea is to design using natural language and concepts of domains, predicates, constraints, sets, set operations, and relations.

The logical design process is database agnostic; for the initial code samples I will use PostgreSQL, which can later be translated to other SQL dialects.

Domains

A domain is simply a set of all possible values over which a variable of interest may range.

The board is composed of 64 named squares, organised in eight rows and eight columns; rows and columns are labelled.

square_name = {'a1' .. 'h8'} -- set of square names
row_lbl     = {'1'  .. '8'}  -- set of row labels
col_lbl     = {'a'  .. 'h'}  -- set of column labels

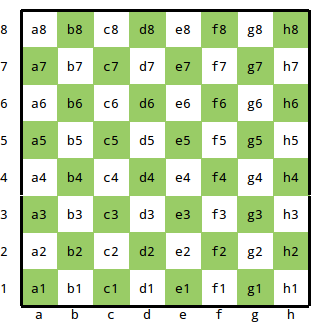
It is convenient to refer to a square by Continue reading “Eight Queens in SQL [1]”